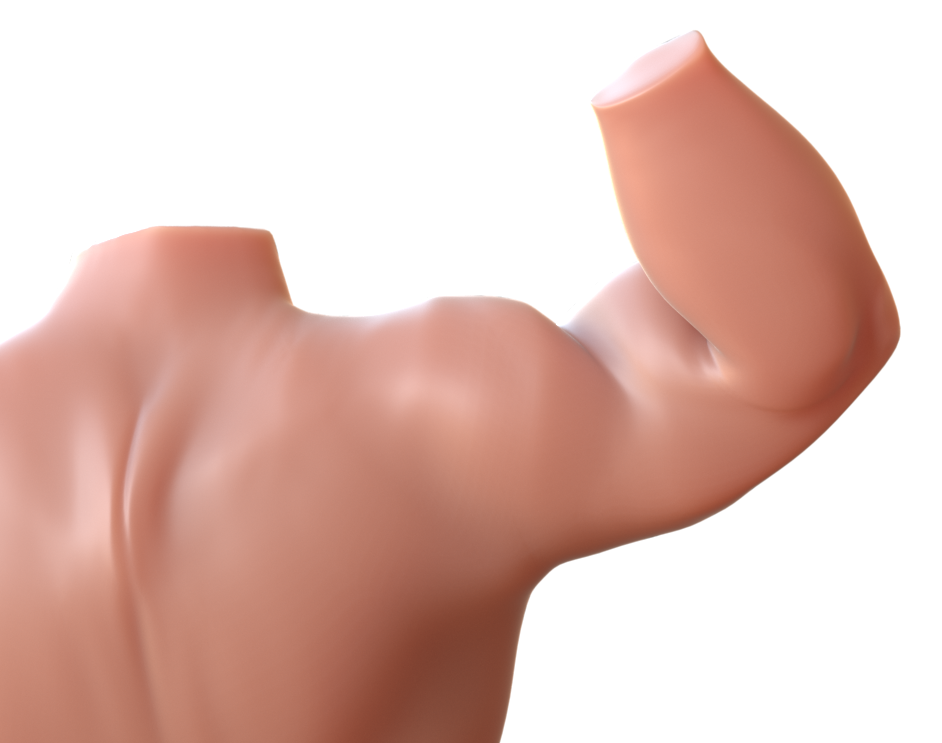
Despite recent progress in developing animatable full-body avatars, realistic modeling of clothing - one of the core aspects of human self-expression - remains an open challenge. State-of-the-art physical simulation methods can generate realistically behaving clothing geometry at interactive rates. Modeling photorealistic appearance, however, usually requires physically-based rendering which is too expensive for interactive applications. On the other hand, data-driven deep appearance models are capable of efficiently producing realistic appearance, but struggle at synthesizing geometry of highly dynamic clothing and handling challenging body-clothing configurations. To this end, we introduce pose-driven avatars with explicit modeling of clothing that exhibit both photorealistic appearance learned from real-world data and realistic clothing dynamics. The key idea is to introduce a neural clothing appearance model that operates on top of explicit geometry: at training time we use high-fidelity tracking, whereas at animation time we rely on physically simulated geometry. Our core contribution is a physically-inspired appearance network, capable of generating photorealistic appearance with view-dependent and dynamic shadowing effects even for unseen body-clothing configurations. We conduct a thorough evaluation of our model and demonstrate diverse animation results on several subjects and different types of clothing. Unlike previous work on photorealistic full-body avatars, our approach can produce much richer dynamics and more realistic deformations even for many examples of loose clothing. We also demonstrate that our formulation naturally allows clothing to be used with avatars of different people while staying fully animatable, thus enabling, for the first time, photorealistic avatars with novel clothing.

Dressing Avatars: Deep Photorealistic Appearance for Physically Simulated Clothing
Donglai Xiang, Timur Bagautdinov, Tuur Stuyck, Fabian Prada, Javier Romero, Weipeng Xu, Shunsuke Saito, Jingfan Guo, Breannan Smith, Takaaki Shiratori, Yaser Sheikh, Jessica Hodgins, Chenglei Wu
ACM Transaction on Graphics (Proceedings of SIGGRAPH Asia 2022)

We present a robust learning algorithm to detect and handle collisions in 3D deforming meshes. We first train a neural network to detect collisions and then use a numerical optimization algorithm to resolve penetrations guided by the network. Our learned collision handler can resolve collisions for unseen, high-dimensional meshes with thousands of vertices. To obtain stable network performance in such large and unseen spaces, we apply active learning by progressively inserting new collision data based on the network inferences. We automatically label these new data using an analytical collision detector and progressively fine-tune our detection networks. We evaluate our method for collision handling of complex, 3D meshes coming from several datasets with different shapes and topologies, including datasets corresponding to dressed and undressed human poses, cloth simulations, and human hand poses acquired using multi-view capture systems.

N-Penetrate: Active Learning of Neural Collision Handler for Complex 3D Mesh Deformations
Qingyang Tan, Zherong Pan, Breannan Smith, Takaaki Shiratori, Dinesh Manocha
International Conference on Machine Learning 2022

hand_tracking.png

Many of the actions that we take with our hands involve self- contact and occlusion: shaking hands, making a fist, or interlacing our fingers while thinking. This use of of our hands illustrates the importance of tracking hands through self-contact and occlusion for many applications in computer vision and graphics, but existing methods for tracking hands and faces are not designed to treat the extreme amounts of self-contact and self-occlusion exhibited by common hand gestures. By extending recent advances in vision-based tracking and physically based animation, we present the first algorithm capable of tracking high-fidelity hand deformations through highly self-contacting and self-occluding hand gestures, for both single hands and two hands. By constraining a vision-based tracking algorithm with a physically based deformable model, we obtain an algorithm that is robust to the ubiquitous self-interactions and massive self-occlusions exhibited by common hand gestures, allowing us to track two hand interactions and some of the most difficult possible configurations of a human hand.

Constraining Dense Hand Surface Tracking with Elasticity
Breannan Smith, Chenglei Wu, He Wen, Patrick Peluse, Yaser Sheikh, Jessica K. Hodgins, Takaaki Shiratori
ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2020)

analytical_teaser.png

Many strategies exist for optimizing non-linear distortion energies in geometry and physics applications, but devising an approach that achieves the convergence promised by Newton-type methods remains challenging. In order to guarantee the positive semi-definiteness required by these methods, a numerical eigendecomposition or approximate regularization is usually needed. In this paper, we present analytic expressions for the eigensystems at each quadrature point of a wide range of isotropic distortion energies. These systems can then be used to project energy Hessians to positive semi-definiteness analytically. Unlike previous attempts, our formulation provides compact expressions that are valid both in 2D and 3D, and does not introduce spurious degeneracies. At its core, our approach utilizes the invariants of the stretch tensor that arises from the polar decomposition of the deformation gradient. We provide closed-form expressions for the eigensystems for all these invariants, and use them to systematically derive the eigensystems of any isotropic energy. Our results are suitable for geometry optimization over flat surfaces or volumes, and agnostic to both the choice of discretization and basis function. To demonstrate the efficiency of our approach, we include comparisons against existing methods on common graphics tasks such as surface parameterization and volume deformation.

Analytic Eigensystems for Isotropic Distortion Energies
Breannan Smith, Fernando de Goes, Theodore Kim
ACM Transactions on Graphics

We propose a technique to simulate granular materials that exploits the dual strengths of discrete and continuum treatments. Discrete element simulations provide unmatched levels of detail and generality, but prove excessively costly when applied to large scale systems. Continuum approaches are computationally tractable, but limited in applicability due to built-in modeling assumptions; e.g., models suitable for granular flows typically fail to capture clogging, bouncing and ballistic motion. In our hybrid approach, an oracle dynamically partitions the domain into continuum regions where safe, and discrete regions where necessary. The domains overlap along transition zones, where a Lagrangian dynamics mass-splitting coupling principle enforces agreement between the two simulation states. Enrichment and homogenization operations allow the partitions to evolve over time. This approach accurately and efficiently simulates scenarios that previously required an entirely discrete treatment.

Hybrid Grains: Adaptive Coupling of Discrete and Continuum Simulations of Granular Media
Yonghao Yue, Breannan Smith, Peter Yichen Chen, Maytee Chantharayukhonthorn, Ken Kamrin, Eitan Grinspun
ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia 2018)

Non-linear hyperelastic energies play a key role in capturing the fleshy appearance of virtual characters. Real-world, volume-preserving biological tissues have Poisson's ratios near 1/2, but numerical simulation within this regime is notoriously challenging. In order to robustly capture these visual characteristics, we present a novel version of Neo-Hookean elasticity. Our model maintains the fleshy appearance of the Neo-Hookean model, exhibits superior volume preservation, and is robust to extreme kinematic rotations and inversions. We obtain closed-form expressions for the eigenvalues and eigenvectors of all of the system's components, which allows us to directly project the Hessian to semi-positive-definiteness, and also leads to insights into the numerical behavior of the material. These findings also inform the design of more sophisticated hyperelastic models, which we explore by applying our analysis to Fung and Arruda-Boyce elasticity. We provide extensive comparisons against existing material models.

Stable Neo-Hookean Flesh Simulation
Breannan Smith, Fernando de Goes, Theodore Kim
ACM Transactions on Graphics

Iterative algorithms are frequently used to resolve simultaneous impacts between rigid bodies in physical simulations. However, these algorithms lack formal guarantees of termination, which is sometimes viewed as potentially dangerous, so failsafes are used in practical codes to prevent infinite loops. We show such steps are unnecessary. In particular, we study the broad class of such algorithms that are conservative and satisfy a minimal set of physical correctness properties, and which encompasses recent methods like Generalized Reflections as well as pairwise schemes. We fully characterize finite termination of these algorithms. The only possible failure cases can be detected, and we describe a procedure for modifying the algorithms to provably ensure termination. We also describe modifications necessary to guarantee termination in the presence of numerical error due to the use of floating-point arithmetic. Finally, we discuss the challenges dissipation introduce for finite termination, and describe how dissipation models can be incorporated while retaining the termination guarantee.

All’s Well That Ends Well: Guaranteed Resolution of Simultaneous Rigid-Body Impact
Etienne Vouga, Breannan Smith, Danny M. Kaufman, Rasmus Tamstorf, Eitan Grinspun
ACM Transactions on Graphics (Proceedings of SIGGRAPH 2017)

We consider the simulation of dense foams composed of microscopic bubbles, such as shaving cream and whipped cream. We represent foam not as a collection of discrete bubbles, but instead as a continuum. We employ the Material Point Method (MPM) to discretize a hyperelastic constitutive relation augmented with the Herschel-Bulkley model of non-Newtonian plastic flow, which is known to closely approximate foam behavior. Since large shearing flows in foam can produce poor distributions of material points, a typical MPM implementation can produce non-physical internal holes in the continuum. To address these artifacts, we introduce a particle resampling method for MPM. In addition, we introduce an explicit tearing model to prevent regions from shearing into artificially-thin, honey-like threads. We evaluate our method's efficacy by simulating a number of dense foams, and we validate our method by comparing to real-world footage of foam.

Continuum Foam: A Material Point Method for Shear-Dependent Flows
Yonghao Yue, Breannan Smith, Christopher Batty, Changxi Zheng, Eitan Grinspun
ACM Transactions on Graphics

We develop an algorithm for the efficient and stable simulation of large-scale elastic rod assemblies. We observe that the time-integration step is severely restricted by a strong nonlinearity in the response of stretching modes to transversal impact, the degree of this nonlinearity varying greatly with the shape of the rod. Building on these observations, we propose the ADONIS collision response algorithm that adapts the degree of nonlinearity in impact solves. We illustrate the advantages of the ADONIS algorithm by analyzing simulations involving elastic rod assemblies of varying density and scale, with up to 1.7 million individual contacts per time step.

Adaptive Nonlinearity for Collisions in Complex Rod Assemblies
Danny M. Kaufman, Rasmus Tamstorf, Breannan Smith, Jean-Marie Aubry, Eitan Grinspun
ACM Transactions on Graphics (Proceedings of SIGGRAPH 2014)

Resolving simultaneous impacts is an open and significant problem in collision response modeling. Existing algorithms in this domain fail to fulfill at least one of five physical desiderata. To address this we present a simple generalized impact model motivated by both the successes and pitfalls of two popular approaches: pair-wise propagation and linear complementarity models. Our algorithm is the first to satisfy all identified desiderata, including simultaneously guaranteeing symmetry preservation, kinetic energy conservation, and allowing break-away. Furthermore, we address the associated problem of inelastic collapse, proposing a complementary generalized restitution model that eliminates this source of nontermination. We then consider the application of our models to the synchronous time-integration of large-scale assemblies of impacting rigid bodies. To enable such simulations we formulate a consistent frictional impact model that continues to satisfy the desiderata. Finally, we validate our proposed algorithm by correctly capturing the observed characteristics of physical experiments including the phenomenon of extended patterns in vertically oscillated granular materials.

Reflections on Simultaneous Impact
Breannan Smith, Danny M. Kaufman, Etienne Vouga, Rasmus Tamstorf, Eitan Grinspun
ACM Transactions on Graphics (Proceedings of SIGGRAPH 2012)

We develop a method for reliable simulation of elastica in complex contact scenarios. Our focus is on firmly establishing three parameter-independent guarantees: that simulations of well-posed problems (a) have no interpenetrations, (b) obey causality, momentum- and energy-conservation laws, and (c) complete in finite time. We achieve these guarantees through a novel synthesis of asynchronous variational integrators, kinetic data structures, and a discretization of the contact barrier potential by an infinite sum of nested quadratic potentials. In a series of two- and three dimensional examples, we illustrate that this method more easily handles challenging problems involving complex contact geometries, sharp features, and sliding during extremely tight contact.

Asynchronous Contact Mechanics
David Harmon, Etienne Vouga, Breannan Smith, Rasmus Tamstorf, Eitan Grinspun
ACM Transactions on Graphics (Proceedings of SIGGRAPH 2009)

Asynchronous Contact Mechanics
David Harmon, Etienne Vouga, Breannan Smith, Rasmus Tamstorf, Eitan Grinspun
Communications of the ACM, Volume 55, Issue 4, April 2012, Pages 102-109